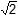Study Guide
Field 202: Middle Grades left paren 5 to 8 right paren Mathematics
Sample Multiple-Choice Questions
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
The following reference material will be available to you during the test:
Each multiple-choice question has four answer choices. Read each question and its answer choices carefully and choose the ONE best answer.
During the test you should try to answer all questions. Even if you are unsure of an answer, it is better to guess than not to answer a question at all. You will NOT be penalized for choosing an incorrect response.
Objective 0001
Understand calculus.
1. The graph of a parabola intersects the x-axis when X equals 4 and X equals negative 1. If the y-intercept is a positive number, which of the following equations could represent this graph?
- Y equals, 2, left paren, X minus 4, right paren, left paren, X plus 1, right paren
- Y equals, negative 2, left paren, X minus 4, right paren, left paren, X plus 1, right paren
- Y equals, 2, left paren, X plus 4, right paren, left paren, X minus 1, right paren
- Y equals, negative 2, left paren, X plus 4, right paren, left paren, X minus 1, right paren
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
A polynomial function factored in the form Y equals, A, left paren, B X plus or minus C, right paren, left paren, D X plus or minus E, right paren will have x-intercepts when B X plus or minus C equals 0, D X plus or minus E equals 0, or A equals 0. The graph of the polynomial will open upward if A is greater than 0. and downward if A is less than 0. For the polynomial to have the given x-intercepts of X equals 4 and X equals negative 1, left paren X minus 4 right paren and left paren X plus 1 right paren must be binomial factors. The y-intercept is a positive number, so the graph of the polynomial will open downward; thus, A is less than 0. The function Y equals, negative 2, left paren, X minus 4, right paren, left paren, X plus 1, right paren satisfies these conditions.
Objective 0001
Understand calculus.
2. Which of the following equations should be solved to find the x-coordinates of the maximum or minimum points of the function y equals left paren x squared minus 3 right paren squared?
- 2 left paren x squared minus 3 right paren equals 0
- 2 x left paren x squared minus 3 right paren equals 0
- 4 left paren x squared minus 3 right paren equals 0
- 4 x left paren x squared minus 3 right paren equals 0
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
The maximum or minimum values of any continuous function y are found by calculating the derivative left paren d y over d x right paren of the function, setting the derivative equal to zero, and solving this equation for x. The maxima and minima of function y will occur at these x values. The product rule can be used to find the derivative of y. If y equals left paren x squared minus 3 right paren squared equals left paren x squared minus 3 right paren left paren x squared minus 3 right paren, then d y over dx equals left paren x squared minus 3 right paren 2 x plus 2x left paren x squared minus 3 right paren equals 4 x left paren x squared minus 3 right paren. The minimum or maximum values of function y can be found by finding the x-values that solve 4 x left paren x squared minus 3 right paren equals 0. Note: the chain rule may also be used to find the derivative of function y in this case.
Objective 0002
Understand college statistics.
3. A student's median score on three tests is 87. The mean of the student's scores is 89, and the range is 6. Which of the following scores could be one of the student's other two test scores?
- 85
- 86
- 90
- 93
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
The median is found by ordering all observations numerically and then locating the middle observation, and the mean is found by summing the values of all observations and dividing the sum by the number of observations. In this case the order of the observations is: a, 87, b. The mean is 89; therefore , a plus 87 plus b over 3 which yields a plus b equals 180. The range is the difference between the maximum and minimum values; that is, b minus a equals 6 Using elimination, solve the system a plus b equals 180 and b minus a equals 6 to obtain a equals 87 and b equals 93 so 93 is one of the student's other two test scores.
Objective 0003
Understand ratios and proportional relationships.
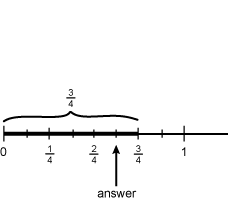
4. Use the diagram below to answer the question that follows.
The number line shown best models which of the following fraction computation problems?
- five sixth times 3 fourths
- 3 fourths minus five eighths
- five eighths divided by 1 eighths
- 3 fourths minus five sixth
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
The number line shows 5 sixth of the fraction 3 fourths shaded. This indicates multiplication. The correct response is 5 sixth times 3 fourths.
Objective 0003
Understand ratios and proportional relationships.
5. Property taxes in a particular community are calculated on an amount equal to 70 percent of the market value of the property. In this community, the tax rate for this year is 30 dollars per 1,000 dollars of taxable value. If a homeowner's property tax bill is 5,250 dollars, what is the market value of the home?
- 204,750 dollars
- 227,500 dollars
- 235,000 dollars
- 250,000 dollars
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
The town calculates the property tax by charging 30 dollars for each 1000 dollars of taxable value; that is, property tax equals 30 thousandths left paren taxable value right paren. The property tax on this home is 5,250 dollars. After substituting 5,250 dollars in for property tax, solve for taxable value to find taxable value equals 5,250 dollars. The taxable value is equal to 70 percent of the market value; that is, taxable value equals 0.70 left paren market value right paren. After substituting 5,250 dollars in for taxable value, solve for market value to find market value equals 250,000 dollars. The market value of this home is 250,000 dollars.
Objective 0004
Understand the structure and properties of the real number system.
6. Use the Venn diagram below to answer the question that follows.
the venn diagram has 2 circles, labeled a and b. circle a contains the values x and y squared. circle b contains the value z cubed. the intersection contains the values x cubed and z.
The Venn diagram shown represents the prime factorization of two integers A and B. Based on the diagram, which of the following expressions is the quotient of the least common multiple divided by the greatest common factor of A and B?
- x cubed times z
- x times y squared times z
- x times y squared times z cubed
- x cubed times y squared times z cubed
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
The least common multiple (LCM) of A and B is the smallest positive integer that is divisible by both A and B; it can be found by finding the prime factorizations of A and B and multiplying together the prime numbers with the highest exponents from both A and B. The prime factorizations of A and B are x to the power of 4 y squared z to the power of 4 and x cubed z to the power of 4 respectively. The prime numbers with the highest exponents are x to the power of 4, y squared, z to the power of 4, so the LCM is x to the power of 4 y squared z to the powre of 4. The greatest common factor (GCF) of A and B is the greatest factor that divides both A and B; this is the intersection of A and B in the Venn diagram, x cubed z Therefore, l c m over g c f equals x to the power of 4 y squared z to the power of four over x cubed z equals x y squared z cubed
Objective 0005
Understand expressions and equations.
7. A textbook recommends that factoring polynomials in the form x squared plus b x plus c be taught before factoring polynomials in the form a x squared plus b x plus c. A teacher decides to skip x squared plus b x plus c and move directly to factoring polynomials in the form a x squared plus b x plus c. Which of the following statements describes the best reason for doing this?
- The curriculum minimizes factoring polynomials in the form x squared plus b x plus c because expressions like a x squared plus b x plus c are more essential to algebra.
- The students will benefit from the rigor of practicing the more difficult factoring techniques involved in factoring polynomials in the form a x squared plus b x plus c.
- The process for factoring polynomials in the form a x squared plus b x plus c is equivalent to the process for factoring polynomials in the form x squared plus b x plus c.
- The teacher wants to give the students more opportunities to ask questions, which factoring polynomials in the form a x squared plus b x plus c will do.
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
The process for factoring polynomials in the form x squared plus bx plus c is equivalent to factoring polynomials in the form a x squared plus b x plus c when a equals 1. By factoring a x squared plus bx plus c first, students are less likely to misinterpret the process of factoring when a equals 1 as a separate factoring procedure from factoring when a not equal to 1. Skipping x squared plus b x plus c and moving to a x squared plus b x plus c allows students to deduce that a equals 1 when such examples arise.
Objective 0006
Understand relations and functions.
8. The points left paren B comma C right paren and left paren 1 comma A right paren are on the graph of a directly proportional relationship between variables y and x. Which of the following equations expresses a valid relationship between left paren B comma C right paren and left paren 1 comma A right paren ?
- C minus A, over, B minus 1, equals 1
- C minus A, over, B minus 1, equals Y
- C minus A, over, B minus 1, equals A
- C minus A, over, B minus 1, equals X
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
When two variables x and y vary directly, there is a number m such that Y equals M X, with m representing the slope of the line containing the variables. The slope, m, between any two points on the line, left paren X sub 1 comma Y sub 1 right paren and left paren X sub 2 comma Y sub 2 right paren is a constant, M equals, Y sub 1 minus Y sub 2, over, X sub 1 minus X sub 2 which for the points left paren B comma C right paren and left paren 1 comma A right paren is calculated as M equals C minus A over B minus 1. Substituting the constant m and the values X equals 1 and Y equals A in the equation Y equals M X gives left paren, C minus A, over, B minus 1, right paren, left paren, 1, right paren, equals, left paren, C minus A, over, B minus 1, right paren.
Objective 0006
Understand relations and functions.
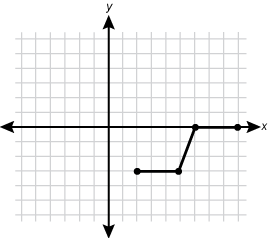
9. Use the graph below to answer the question that follows.
the graph is an x, y graph with a grid and with no values marked. a line is plotted from 2 squares to the left of the y axis and 1 square below the x axis, to 1 square to the right of the y axis and 1 square below the x axis, to 2 squares to the right of the y axis and 2 squares above the x axis, to 5 squares to the right of the y axis and 2 squares above the x axis.
The graph above represents the function f(x). Which of the following graphs represents the function f left paren x minus 2 right paren plus 4.
Each response is the same graph with the function shifted.
-
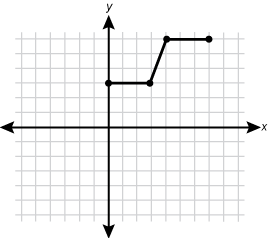 The function is shifted 2 squares to the right and 4 squares up.
The function is shifted 2 squares to the right and 4 squares up. -
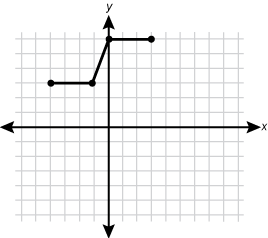 The function is shifted 2 squares to the left and 4 squares up.
The function is shifted 2 squares to the left and 4 squares up. -
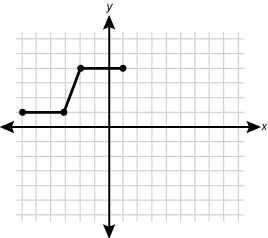 The function is shifted 4 squares to the left and 2 squares up.
The function is shifted 4 squares to the left and 2 squares up. -
 The function is shifted 4 squares to the right and 2 squares down.
The function is shifted 4 squares to the right and 2 squares down.
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
The transformation g left paren x right paren right arrow g left paren x minus h right paren denotes a horizontal shift h units to the right in the graph of g(x), and g left paren x right paren right arrow g left paren x right paren plus k denotes a vertical shift k units up. Therefore, f left paren x right paren right arrow f left paren x minus 2 right paren plus 4 denotes a horizontal shift 2 units to the right and a vertical shift 4 units up for f left paren x right paren. Graph A represents this transformation.
Objective 0007
Understand linear functions and relations.
10. A tutor charges a flat fee per session and then an hourly rate. For a 2-hour session, the charge is 100 dollars and for a 6-hour session, the charge is 268 dollars. At this same rate, what is the charge for a 7-hour session?
- 294 dollars
- 310 dollars
- 315 dollars
- 350 dollars
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
The situation can be modeled by the equation charge equals flat fee plus hour left paren rate right paren. For a 2-hour session, the equation is 100 equals flat fee plus 2 left paren rate right paren and for a 6-hour session, the equation is 268 equals flat fee plus 6 left paren rate right paren. This yields the system of equations f plus 2 r equals 100 over f plus 6 r equals 268, which can be solved using elimination: illustration of the solution f plus 2 r equals 100 is negated and added to f plus 6 r equals 268 resulting in 4 r equals 168. Thus, r equals 42 and f equals 16. The model the tutor uses is charge equals 16 plus 42 left paren hour right paren. To determine how much the tutor charges for a 7-hour session, substitute hour equals 7 into the model, and find charge equals 310. The tutor charges 310 dollars for a 7-hour session.
Objective 0008
Understand nonlinear functions.
11. Which of the following statements describes the roots of the equation y equals x squared plus four x plus 4?
- There are 2 distinct real roots.
- There is 1 real double root.
- There are 2 distinct imaginary roots.
- There is 1 imaginary and 1 real root.
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
The discriminant, b squared minus 4 a c of a quadratic function in the form y equals a x squared plux b x plus c can be used to determine the number of roots of the function. In y equals x squared plus 4 x plus 4, a equals 1, b equals 4, and c equals 4 Substitute these values into b squared minus 4 a c to yield left paren 4 right paren squared minus 4 left paren 1 right paren left paren 4 right paren equals 0. When the discriminant is 0, there is one real root. In this case, y equals left paren x plus 2 right paren left paren x plus 2 right paren, so there is one double root, x equals negative 2.
Objective 0009
Understand the principles of two- and three-dimensional geometry.
12. Use the diagram below to answer the question that follows.
The diagram shows a circle with 2 radial lines and a cord connecting the points where the radial lines intersect the edge of the circle. One radial line is labeled 2 centimeters.
A triangle is drawn in the interior of a circle whose radius measures 2 c m, as shown in the diagram. The central angle measures 60 degrees. The triangle is approximately what percentage of the circle?
- 14 percent
- 16 percent
- 28 percent
- 32 percent
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
The percent that the triangle is of the circle can be represented by area sub triangle over area sub circle. The total area of a circle with radius 2 centimeters is area sub circle equals pi r squared equals 4 pi c m squared The area of the triangle can be found by first determining the height h of the triangle and then using the area formula for triangles. Because the central angle is 60 degrees and two sides of the triangle are radii, the triangle is equilateral. The perpendicular segment from any vertex to the opposite side will create a 30-60-90 special right triangle with shortest leg measuring 1 cm and hypotenuse measuring 2 cm. Using special right triangle properties, or the Pythagorean formula, the height h of the triangle is the square root of 3 cm. Thus, area sub triangle equals b h over 2 equals 2 times the square root of 3 over 2 equals the square root of three centimeters squared so Area sub triangle over area sub circle equals the square root of 3 over 4 pi equals 0.138 The triangle is approximately 14 percent of the circle.
Objective 0009
Understand the principles of two- and three-dimensional geometry.
13. Use the diagram below to answer the question that follows.
the diagram shows a right square pyramid. the apex is point a. the vertices of the base are points b, c, d, and e. the center point of the base is point f. the altitude from f to a is dimensioned as 3 inches. the edge from point a to point c is labeled edge.
The wooden block shown has the shape of a right square pyramid. The volume of the block is 4 cubic inches and its height is 3 inches. What is the length of edge a c ?
- the square root of 5 inches
- the square root of 8 inches
- the square root of 11 inches
- the square root of 13 inches
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
The volume of a square pyramid is v equals s squared h over 3 where s is the side length of the base and h is the height of the pyramid. Substituting 4 and 3 into the formula for V and h, respectively, 4 equals s squared left paren 3 right paren over 3 Solve for s to obtain s equals 2 inches. If e d equals d c equals 2,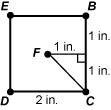 a diagram shows the square base of the pyramid,
with the vertices labeled b, c, d, and e and point f in the center. side cd is dimensioned
as 2 inches. a line has been drawn from point f to edge bc, at a right angle to
edge bc. this line is dimensioned as 1 inch, and the segments of side bc on either
side of this line are each dimensioned as 1 inch. another line has been drawn from
point f to the vertex point c, forming a right triangle with vertices at f, c, and
the midpoint of side bc.
then by the Pythagorean theorem
left paren e c right paren squared equals 2 squared plus 2 squared
so
e c equals 2 times the square root of two
inches and
f c equals the square root of two
triangle a f c
can be solved for
a c
using
f c equals the square root of 2
inches and
a f equals 3
inches and substituting into the Pythagorean theorem:
left paren a c right paren squared equals left paren f c right paren squared plus left paren a f right paren squared
and
left paren a c right paren squared equals left paren the square root of 2 right paren squared plus left paren 3 right paren squared
so
a c equals the square root of 11
The length of edge
a c
is
the square root of eleven inches.
a diagram shows the square base of the pyramid,
with the vertices labeled b, c, d, and e and point f in the center. side cd is dimensioned
as 2 inches. a line has been drawn from point f to edge bc, at a right angle to
edge bc. this line is dimensioned as 1 inch, and the segments of side bc on either
side of this line are each dimensioned as 1 inch. another line has been drawn from
point f to the vertex point c, forming a right triangle with vertices at f, c, and
the midpoint of side bc.
then by the Pythagorean theorem
left paren e c right paren squared equals 2 squared plus 2 squared
so
e c equals 2 times the square root of two
inches and
f c equals the square root of two
triangle a f c
can be solved for
a c
using
f c equals the square root of 2
inches and
a f equals 3
inches and substituting into the Pythagorean theorem:
left paren a c right paren squared equals left paren f c right paren squared plus left paren a f right paren squared
and
left paren a c right paren squared equals left paren the square root of 2 right paren squared plus left paren 3 right paren squared
so
a c equals the square root of 11
The length of edge
a c
is
the square root of eleven inches.
Objective 0010
Understand the principles of coordinate and transformational geometries.
14. Use the graph below to answer the question that follows.
the graph is a cartesian graph with values labeled from negative 5 to 5 on both axes. triangle abc is drawn with point a 4 units to the right of the y axis and 5 units above the x axis, point b 4 units to the right of the y axis and 5 units above the x axis, and point c 5 units to the right of the y axis and 1 unit above the x axis.
Triangle ABC is transformed using a translation 6 units down followed by a dilation with scale factor of 2 centered at the origin. Which of the following coordinates are the coordinates of the image point B?
- left paren negative 8 comma negative 6 right paren
- left paren negative 8 comma 6 right paren
- left paren 4 comma negative 6 right paren
- left paren 4 comma 1 right paren
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
Vertical translations of k units on the point left paren x comma y right paren can be described by left paren x comma y right paren right arrow left paren x comma y plus or minus k right paren. Dilations undergoing a scale factor of j and centered at the origin can be described by left paren x comma y right paren right arrow left paren j x comma j y right paren. B is at left paren 2 comma 3 right paren and is transformed 6 units down, so the initial image of B is located at left paren 2 comma negative 3 right paren Then, this image is dilated by a scale factor of 2 centered at the origin, so the final image of point B is located at left paren 4 comma negative 6 right paren
Objective 0011
Understand the principles and techniques of probability.
15. A parent and a child are playing a game. Each rolls a standard six-sided die to determine who has the first turn in the game. What is the probability that the child rolls a higher number than the parent?
- 1 half
- 7 eighths
- four ninths
- 5 twelfths
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
Three outcomes are possible: the parent rolls a number greater than the child, the child rolls a number greater than the parent, or the parent and the child roll the same number; this can be described by P left paren child roll equals parent roll right paren plus P left paren child roll is greater than parent roll right paren plus p left paren parent roll is greater than child roll right paren equals 1. The probability of any given number being rolled is , 1 sixth so the probability the parent and child roll the same number is 1 sixth. It is equally likely that the parent or child rolls the higher value. Thus, the probability of all outcomes can be re-expressed as 1 sixth plus 2 p left paren child roll is greater than parent roll right paren equals 1, and can be solved to find p left paren child roll is greater than parent roll right paren equals 5 twelfths. The probability the child rolls higher than the parent is 5 twelfths.
Objective 0012
Understand the principles and techniques of statistics.
16. Use the boxplot below to answer the question that follows.
the box plot has tick marks in increments of 2, labeled from 70 to 100 in increments of 10. the minimum line is at 78, the left edge of the box is at 80, the line inside the box is at 82, the right edge of the box is at 90, and the maximum line is at 100.
After a recent test, a teacher created a boxplot to display the scores of the 20 students in the class. Based on the information in the boxplot, which of the following measures has the highest value for the set of test scores?
- mean
- median
- range
- standard deviation
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
the portion of the graph representing the upper 50 percent of the data left paren 82 to 100 right paren is considerably larger than the portion of the graph represented by the lower 50 percent of the data left paren 78 to 82 right paren. This indicates that the distribution of scores is skewed towards the high end, so there are some very high values. These high values will raise the mean, whereas the median is virtually unaffected by a few such values. Therefore, the mean is probably higher than the median.
Objective 0012
Understand the principles and techniques of statistics.
17. Students are directed to make twelve displays: a boxplot, a stem plot, and a histogram, one for each of four different sets of data. This exercise particularly reinforces application skills because it helps students:
- remember how to construct each type of display through repeated practice.
- select the most appropriate type of data display for different types of data sets.
- recognize how different displays may present misleading graphs and statistics.
- understand how the strength of a correlation is shown by different displays.
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
Boxplots, stem plots, and histograms are different methods of displaying quantitative data. Boxplots are generally used for comparing the overall distribution of several groups and for displaying outliers. Histograms are appropriate for viewing the distribution of large sets of data because they can be created efficiently, while stem plots are less efficient for large sets of data because they must show individual values. This exercise allows students to compare and contrast the effectiveness of each type of display when used with different types of data sets.
Objective 0013
Apply knowledge of foundations of research-based disciplinary literacy instruction
and assessment.
18. As compared with the narrative texts (stories) that middle school students encounter in an English language arts class, the story problems students encounter in mathematics class are often more difficult to comprehend, especially if the students are not native speakers of English. According to research, which of the following statements best explains a research-based rationale for this phenomenon?
- Story problems are more likely to require students to make text-to-self and text-to-world connections in order to determine a story's key idea or theme.
- Story problems are typically short and about random topics, so they often lack contextual clues to help students understand unfamiliar vocabulary and situations.
- Students are more likely to encounter complex syntax and semantic features not used in everyday spoken language when reading story problems than when reading literary texts.
- Students often do not realize that they have to apply the same skills and strategies when analyzing story problems as they do when analyzing literary texts.
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
All students use a variety of comprehension and vocabulary strategies when they are reading. These strategies are of particular importance for English language learners who rely on them to understand the content presented in discipline-specific texts. According to current research, one such vocabulary strategy is the use of contextual clues in the text (e.g., descriptions, examples, definitions, synonyms) to aid in determining the meaning of an unknown word or concept. Math story problems are typically short and about random topics, activities, or situations that may be wholly unfamiliar to students, particularly students for whom English is a new language. The text of story problems often does not include sufficient context to provide students with clues to understanding such unfamiliar vocabulary and situations.
Objective 0014
Apply knowledge of academic-language and vocabulary development to support students'
disciplinary literacy development in the mathematics classroom.
19. To promote students' vocabulary and concept development related to quadrilaterals, a middle school mathematics teacher guides students in comparing diagrams of six common four-sided figures. First, students identify and discuss the features of each figure. Then, they draw their own pictures of the quadrilaterals. Finally, the teacher leads students in constructing a semantic features analysis chart. A copy of their completed chart is shown below.
Quadrilaterals Term Four Sides All Sides of Equal Length All Angles Equal Opposite Sides of Equal Length Opposite Sides Parallel Two Sets of Parallel Sides Rectangle plus minus plus plus plus plus Square plus plus plus plus plus plus Rhombus plus plus minus plus plus plus Parallelogram plus minus minus plus plus plus Trapezoid plus minus minus minus minus minus Scalene Quadrilateral plus minus minus minus minus minus
In this mathematics lesson, the teacher addresses the diverse strengths and needs of all students primarily by:
- simplifying target academic vocabulary into simpler, everyday words.
- breaking up a complex, multi-layered concept into smaller, more accessible parts.
- using multiple language modalities and viewing to reinforce target content.
- differentiating instruction for students who fail to meet objectives following initial instruction.
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
By using a variety of modalities in this lesson (i.e., viewing diagrams of the quadrilaterals; discussing the features of each quadrilateral; drawing pictures of the quadrilaterals; and using listening, speaking, reading, and writing to construct a semantic features analysis chart), the teacher helps promote the students' understanding of the characteristics of quadrilaterals by addressing a range of learning styles and responding to the diverse strengths and needs of all students. Finally, the semantic features analysis chart the class created helps reinforce the new vocabulary. In the far left column of the chart is a list of terms to be compared, while across the top is a list of properties that the objects might share. The activity helps students compare features of objects that are in the same category by providing a visual prompt of their similarities and differences. It helps them see how similar words are related and connected and is a good visual tool to use with diverse learners for this purpose.
Objective 0016
Apply knowledge of the development of writing, listening, and speaking skills to
support students' disciplinary literacy development in the mathematics classroom.
20. A middle school mathematics teacher wants to incorporate more writing into the mathematics curriculum. Research suggests that which of the following types of writing activities is most effective in developing students' understanding of mathematics concepts and skills?
- asking students routinely to write down the steps they followed to solve each mathematics problem
- providing students with regular brief written feedback on their mathematics work that emphasizes positive reinforcement with minimal elaboration
- asking students routinely to provide descriptive feedback to their peers on the peers' mathematics work
- providing students with regular modeling and guided practice in how to describe mathematics ideas in writing and through graphic organizers
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
The process of writing requires active engagement on the part of students as they must take in, organize, and process information. Current research shows that requiring and encouraging students to write across the curriculum helps to develop an understanding of the content-area concepts and skills they are learning and expands their literacy skills. Since students may be unfamiliar with this type of informational writing, research shows that it is beneficial for the teacher to provide instructional writing support (e.g., teacher modeling, guided practice, use of graphic organizers) until students internalize the process and are able to write appropriate math responses independently.

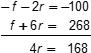 .
.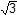 cm.
cm.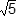 inches
inches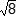 inches
inches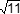 inches
inches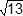 inches
inches