Study Guide
Field 208: Mathematics
Sample Multiple-Choice Questions
Recommendation for individuals using a screenreader: please set your punctuation settings to "most."
Each multiple-choice question has four answer choices. Read each question and its answer choices carefully and choose the ONE best answer.
During the test you should try to answer all questions. Even if you are unsure of an answer, it is better to guess than not to answer a question at all. You will NOT be penalized for choosing an incorrect response.
Objective 0001
Understand mathematical practices.
1. Which of the following tasks can be completed by finding the determinant of a matrix?
- finding the probability of an event modeled by a normal curve
- modeling the exponential increase of a population over time
- finding the area of a polygon described on a coordinate plane
- calculating the greatest common factor of a set of integers
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
Matrices can be used to find the area of a polygon whose vertices are given as coordinate pairs by dividing the polygon into non-overlapping triangles and summing the areas of the triangles. The area of each triangle is found by subtracting pairs of x-coordinates and pairs of y-coordinates to represent two of its sides as vectors: less than symbol A sub 1, B sub 1 greater than symbol and less than symbol A sub 2, B sub 2 greater than symbol. and using the formula Area equals one half times absolute value of matrix of a sub 1, b sub 1, a sub 2, and b sub 2.
Objective 0002
Understand how to select, integrate, and use appropriate technologies in the mathematics
classroom.
2. Software that allows students to create regular tessellations of plane figures would be most appropriate for helping students learn about:
- dilations.
- inversions.
- isometries.
- projections.
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
An isometry is a linear transformation that preserves length. Regular tessellations of a plane are created by reflections, rotations, and translations of plane figures. These transformations all preserve length, thus are isometries.
Objective 0003
Understand the process of reading, and apply knowledge of strategies for promoting
students' reading development in the mathematics classroom.
3. A high school mathematics teacher regularly uses anticipation guides to promote students' disciplinary reading skills. Each anticipation guide consists of carefully constructed statements related to a mathematics topic students will be reading about in their textbook or in a supplemental text. Students must decide whether each statement is true or false based on their prior knowledge. Then, when reading the text, they must identify evidence in the text that either supports or refutes their initial choices. This instructional strategy supports the reading process primarily by:
- motivating students to read informational texts related to mathematics.
- helping students distinguish between fact and opinion in their reading.
- using writing to help deepen students' understanding of their reading.
- fostering in students the habit of applying reasoning during reading.
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
Reading comprehension relies heavily on the ability to make connections not only between pieces of information in a text but between new information being read and the reader's prior knowledge. The instructional strategy described in the scenario requires students to read actively and purposefully to identify evidence in an assigned text that either supports or refutes their prior conceptions about a topic. The students must use metacognition to reflect on what they are reading and apply reasoning to make connections between new and prior knowledge.
Objective 0004
Understand the real number system and its operations.
4. Two containers each hold a number of cubes. The ratio of cubes in container X to those in container Y is 12 to 5. If one-third of the cubes in container X are moved to container Y, there will then be 135 cubes in container Y. What is the total number of cubes in both containers?
- 459
- 351
- 255
- 180
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
One way to solve this is by drawing ratio diagrams. In the first diagram, a strip of 12 boxes compares to a strip of 5 boxes. After one-third of the cubes are moved, the strips have a ratio of 8 to 9.

the diagram shows a graphic representation of this solution method. on the left are 2 strips of squares, representing the containers in the original state. the strip labeled x has 12 squares and the strip labeled y has 5 squares. each square represents a number of cubes. under the last 4 squares in strip y is a curly bracket and the number 1 third, representing the portion of items to be moved to the other container. on the right are 2 strips of squares, representing the containers after some cubes have been moved from container y to container x. the strip is labeled x now has 8 squares, which is the number remaining after 1 third of the original 12 has been removed. the strip labeled y now has 9 squares, which is the result of adding the 4 squares from strip x to the original 5 squares in strip y. below strip y is a curly bracket and the number 135, indicating that these 9 squares represent 135 cubes.
Since 9 boxes represent 135 cubes, each box represents 15 cubes, and the total number of cubes in both boxes is 8 left paren 15 right paren plus 9 left paren 15 right paren equals 255.
Algebraically, let the number of cubes in box x equals 12a and the number in box y equals 5a. Then one third left paren 12 A right paren pluse 5 A equals 135, a equals 15, and 12 left paren 15 right paren plus 5 left paren 15 right paren equals 255.
Objective 0005
Understand the properties of complex numbers and linear algebra.
5. Let z squared?
- 4 left paren cosine pi over 4 plus i sine pi over 4 right paren
- 8 left paren cosine pi over 4 plus i sine pi over 4 right paren
- 4 left paren cosine pi over 2 plus i sine pi over 2 right paren
- 8 left paren cosine pi over 2 plus i sine pi over 2 right paren
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
Computing, z2 = (2 + 2i) (2 + 2i) = 4 + 8i − 4 = 8i. z squared equals left paren 2 plus 2 i right paren left paren 2 plus 2 i right paren equals 4 plus 8 i minus 4 equals 8 i. When graphed on a complex plane, the coordinates of z squared are (0, 8), the point is 8 units from the origin on the imaginary axis, and the angle between the positive real axis and the imaginary axis is 90 degrees or pi over 2 in radians. On a polar graph, this point lies on a circle of radius 8 and its vector makes an angle of pi over 2 with the 0 degrees axis. The polar form of a complex number is z equals r where r is the radius and theta is the angle between the vector represented by z and the 0 degrees axis, so z squared equals 8 left paren cosine pi over 2 plus i sine pi over 2 right paren. alternatively, the polar form of z could be found and demoivre's theorem applied to get the polar form of z squared.
Objective 0005
Understand the properties of complex numbers and linear algebra.
6. Use the information below to answer the question that follows.
Activity: Complex Numbers
Let .
- Find z sub 1 z sub 2
- Find the magnitudes of z sub 1, z sub 2, and z sub 1 z sub 2
- Draw the vectors determined by z sub 1, z sub 2 and z sub 1 z sub 2
- Use a protractor to measure the angles made by each of the three vectors with the positive real axis.
- Make conjectures about the magnitudes and angles of z sub 1, z sub 2 and z sub 1 z sub 2.
As part of a unit on complex numbers, a teacher asks students to complete a series of examples based on the activity shown. This series of examples will enable students to develop an understanding of which of the following processes?
- multiplying complex numbers using their polar forms
- finding the dot product of vectors represented by complex numbers
- demonstrating that multiplication of complex numbers is commutative
- relating the product of the roots of quadratics to complex numbers
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
Using the provided vectors, step 1 in the activity yields z sub 1 z sub 2 equals negative 1 plus 7 i semicolon step 2 yields the absolute value of z sub 1 equals the square root of five, the absolute value of z sub 2 equals the square root of ten, and the absolute value of z sub 1 z sub 2 equals the square root of fifty and steps 3 and 4 yield the graphs of vectors z sub 1 z sub 2 and z sub 1 z sub 2 which have angle measures of approximately theta sub 1 equals 26 degrees theta sub 2 equals 72 degrees and theta sub 1 comma 2 equals 98 degrees as shown.
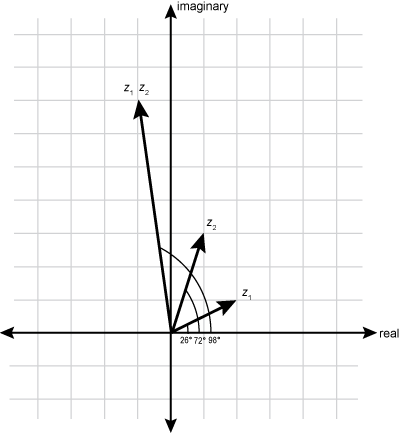
The vectors are shown on a real versus imaginary graph. Vector z sub 1 extends from the origin to a point 2 units to the right and 1 unit up at an angle of 28 degrees . Vector z sub 2 extends from the origin to a point 1 unit to the right and 3 units up at an angle of 72 degrees . Vector z sub 1 z sub 2 extends from the origin to a point 1 unit to the left and 7 units up at an angle of 98 degrees (from the positive real axis).
Inspection shows that 98 degrees equals 26 degrees plus 72 degrees and the square root of fifty equals the square root of five times the square root of ten semicolon that is, theta sub 1 equals theta sub 1 plus theta sub 2 and the absolute value of z sub 1 z sub 2 equals the absolute value of z sub the absolute value of z sub 2 Recall that the magnitude of a vector is equal to the radius, r, of the circle the vector describes, so the absolute value of z sub j equals r sub j That is, this activity enables students to develop an understanding that if z sub 1 equals r sub j left paren cosine theta sub 1 plus i sine theta sub 1 right paren and z sub 2 equals r sub 2 left paren cosine theta sub 2 plus i sine theta sub 2 right paren, then z sub 1 z sub 2 equals r sub 1 r sub 2 left bracket cosine left paren theta sub 1 plus theta sub 2 right paren plus i sine left paren theta sub 1 plus theta sub 2 right paren right bracket which is multiplying the complex numbers z sub 1 and z sub 2 using their polar forms.
Objective 0006
Understand algebraic techniques.
7. Use the table below to answer the question that follows.
x function of x negative 1 0.6667 negative 0.5 0.2667 0 0 .5 negative 0.2667 1 negative 0.6667 1.5 negative 1.714 2 ERROR 2.5 2.222 3 1.2 3.5 0.8485
The table shown could be a partial table of values for which of the following functions?
- function of x equals x over x plus 2
- function of x equals 2x squared over x minus 2
- function of x equals 2x over x squared minus 4
- function of x squared equals x over x squared plus x minus 2
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
A rational function is undefined for some value of x when the denominator of any fraction in the function equals 0. Using the table provided, the function is undefined when x equals 2 semicolon therefore, x minus 2 must be a factor in the denominator. The table shows that when x is negative 0.5 and negative 1, function of x is positive. The function function of x equals 2x over x squared minus 4 can be rewritten as function of x equals 2 x over left paren x minus 2 right paren times left paren x plus 4 right paren which has x minus 2 as a factor in the denominator, and for x equal to negative 0.5 and function of x is positive. Alternatively, calculating f left paren negative 0.5 right paren and f left paren negative 1 right paren for function of x equals 2x over x squared minus 4 yields 0.2667 and 0.6667, respectively.
Objective 0007
Understand functions and the properties of linear relations and functions.
8. Use the graph below to answer the question that follows.
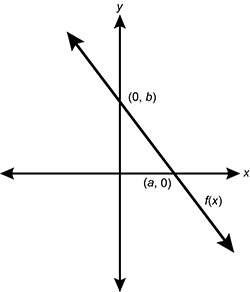
The graph shows f of x plotted on an x, y graph. The line passes through the x axis at point a, 0, and through the y axis at point 0, b.
The function f(x) shown on the graph has intercepts left paren a comma 0 right paren and left paren 0 comma b right paren. Which of the following functions is an equation of its inverse, function f to the power of negative 1
- y equals a over b times x plus b
- y equals a over b times x plus 1
- y equals negative a over b times x plus a
- y equals negative a over b times x plus 1 over b
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
The inverse of a function maps values in the range of a function back to values in the domain. If left paren a comma 0 right paren and left paren 0 comma b right paren are coordinates of points on the line represented by f(x), then left paren 0 comma a right paren and left paren b comma 0 right paren are coordinates of points on the line represented by the inverse function. Calculate slope: 0 minus a over b minus 0 equals negative a over b Using the point-slope form with point left paren b comma 0 right paren y minus 0 equals negative a over b(x minus b) or y equals negative a over b times x plus a.
Objective 0008
Understand quadratic functions and conic sections.
9. The graph of a parabola has an axis of symmetry at x equals 1, an x-intercept at left paren negative 4 comma 0 right paren and a y-intercept at left paren 0 comma negative 12 right paren Which of the following equations represents the graph of this parabola?
- y equals 0.5 left parem x plus 4 right paren left paren x minus 6 right paren
- y equals 0.5 left paren x minus 4 right paren left paren x plus 6 right paren
- y equals left paren x plus 4 right paren left paren x minus 3 right paren
- y equals left paren x minus 4 right paren left paren x plus 3 right paren
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
The intercept form of a parabola is y equals a left paren x minus x sub 1 right paren left paren x minus x sub 2 right paren, where left paren x sub 1 comma 0 right paren and left paren x sub 2 comma 0 right paren are x-intercepts and the axis of symmetry is x equals x sub 1 plus x sub 2 over 2. Because the parabola has an x-intercept at left paren negative 4 comma 0 right paren x sub 1 equals negative 4. Given that the axis of symmetry is x equals 1, and that x sub 1 equals negative 4 1 equals negative 4 plus x sub 2 over 2, so x squared equals 6 Therefore, the equation of the parabola is in the form y equals a left paren x plus 4 right paren left paren x minus 6 right paren. To find a, substitute the values of the coordinate left paren 0, negative 12 right paren into the equation to obtain negative 12 equals a left paren 0 plus 4 right paren left paren 0 plus 6 right paren so a equals 0.5. The equation of the parabola is y equals 0.5 left paren x plus 4 right paren left paren x minus 6 right paren.
Objective 0009
Understand polynomial, absolute value, radical, and rational functions and inequalities.
10. Using dynamic graphing software, a teacher provides an activity in which students are given a function in the form of y equals x to the power of p and students can use a sliding bar to change the value of p. As a student slides the bar, the graph of the function changes. Which of the following statements represents a valid conclusion demonstrated by this activity?
- When p is even, the graph of the function is in the first and second quadrants, and when p is odd, the graph of the function is in the first and third quadrants.
- When p is negative, the graph of the function translates p units to the right, and when p is positive, the graph of the function translates p units to the left.
- When p is less than 1, the graph of the function illustrates decay, and when p is greater than 1 the graph of the function illustrates growth.
- When p is greater than 1 the graph of the function stretches, and when 0 is less than p and p is less than 1 the graph of the function shrinks.
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
The function y equals x to the power of p is a power function. For whole number values of p, when p is even, x to the power of p is positive or zero, so the graph is in the first and second quadrants. When p is odd, x to the power of p will be positive for x is greater than 0, negative for x is less than 0 and 0 when x equals 0. Thus, the graph will lie in the first and third quadrants.
Objective 0009
Understand polynomial, absolute value, radical, and rational functions and inequalities.
11. Given f left paren x right paren equals 3 absolute value of x minus 2 and g left paren x right paren equals 1 half the absolute value of x minus 3 over which of the following intervals on the x-axis is
- left paren negative 7 comma infinity right paren
- left paren negative 7 over 5 comma infinity right paren
- left paren 1 comma infinity right paren
- left paren 1 over 5 comma infinity right paren
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
The vertex of the graph of f left paren x right paren is left paren 0 comma negative 2 right paren its right ray has a slope of 3, and its left ray has a slope of negative 3. The vertex of g left paren x right paren is left paren 3 comma 0 right paren its right ray has a slope of 1 half, and its left ray has a slope of negative 1 half. A sketch of the graphs shows that they intersect once when 0 is less than x is less than 3 and again when x is less than zero. When 0 is less than x and x is less than 3, x is positive so the absolute value of x equals x, but x minus 3 is negative, so the absolute value of x minus 3 equals negative left paren x minus 3 right paren. Solving the inequality 3x minus 2 greater than one half left paren negative x plus 3 right paren for x yields x is greater than 1. When x is less than 0, the absolute value of x equals negative x and the absolute value of x minus 3 equals negative left paren x minus 3 right paren. Solving negative 3x minus 2 greater than one half left paren negative x plus 3 right paren for x yields x less than negative 7 over 5, which is not among the response choices, so the interval asked for is left paren 1 comma infinity right paren
Objective 0010
Understand exponential and logarithmic functions.
12. Atmospheric pressure and altitude are related by the formula ln P over P sub 0 equals negative h over k, where P is pressure in kilopascals at altitude h in kilometers, P sub 0 is pressure at h equals 0, and k is a constant. Which of the following equations expresses P as a function of h?
- P equals negative h over k times P sub 0
- P equals P sub 0 to the power of negative h over k
-
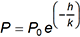 P equals P sub 0 times e to the power of negative h over k
P equals P sub 0 times e to the power of negative h over k
-
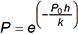 P equals e to the power of negative P sub 0 h over k
P equals e to the power of negative P sub 0 h over k
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
To express P as a function of h, solve the equation In P over P sub 0 = negative h over k for P. Apply the exponential function to both sides of the equation: E to the power of the natural log of P over P sub 0 = e to the power of negative h over k, so P over P sub 0 = e to the power of negative h over k. Multiply both sides of the equation by P sub 0 to obtain P = P sub 0 times e to the power of negative h over k.
Objective 0011
Understand trigonometric functions.
13. How many solutions are there for the system of equations f left paren x right paren equals 3 sine 2 x and g left paren x right paren equals 2 on the interval left bracket 0 comma 2 pi right bracket
- 3
- 4
- 5
- 6
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
The fundamental period of a sine function is 2 pi The graph of f left paren x right paren equals 3 sine 2 x has a period of 2 pi over 2 equals pi thus completing two cycles in the interval left brack 0 comma 2 pi right bracket The amplitude of f left paren x right paren is 3, so the highest value of the function is y equals 3 which will occur twice on this interval. The graph of g left paren x right paren equals 2 is a horizontal line. Since 2 is less than 3 g left paren x right paren intersects f left paren x right paren four times.
Objective 0012
Understand principles of differential calculus.
14. The radius of a spherical balloon is decreasing at the rate of 5 centimeters per second At what rate is the volume of the balloon decreasing when the diameter of the balloon is 20 cm?
- 10,667 pi centimeters cubed per second
- 4,500 pi centimeters cubed per second
- 2,667 pi centimeters cubed per second
- 2,000 pi centimeters cubed per second
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: D.
For a sphere, v equals 4 thirds pi r cubed The rate at which the volume is changing is expressed as the derivative of the volume function with respect to time: d capital V over d t equals 4 pi r squared d r over d t At the time when the diameters equals 20 centimeters and d r over d t equals negative 5 cm per sec, d capital V over d t equals 4 pi left paren 10 squared right paren left paren negative 5 right paren equals negative 2000 pi cm cubed per sec
Objective 0013
Understand principles of integral calculus.
15. A rocket is launched vertically from the ground with an initial acceleration of Its velocity, 250 meters per second squared v, in meters per second at time t is given by v left paren t right paren equals 0.15 t squared plus 250 t What is the height above the ground of the rocket at time equals 6 seconds
- 1,505.4 meters
- 4,510.8 meters
- 6,027.0 meters
- 9,032.4 meters
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
The position function (height) is the antiderivative of the velocity function. Thus, h left paren t right paren equals 0.05 t cubed plus 125 t squared plus c Since the rocket was launched from the ground, h equals zero when t equals zero making c equals 0 as well. Then h left paren 6 right paren equals 0.05 left paren 216 right paren plus 125 left paren 36 right paren equals 4510.8
Objective 0014
Understand principles and applications of measurement.
16. The volume of a cube is 512 cubic inches. What is the ratio of the volume of the sphere that can be inscribed in the cube to the volume of the sphere that can be circumscribed about the cube?
-
1/3
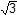 1 over 3 times square root of 3
1 over 3 times square root of 3 -
1/
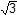 1 over square root of 3
1 over square root of 3 -
1/2
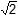 1 over 2 times square root of 2
1 over 2 times square root of 2 -
1/
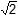 1 over square root of 2
1 over square root of 2
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: A.
The largest sphere that can be inscribed in a cube is tangent to each face of the cube, so its diameter is the length of one side of the cube. Since the volume of the cube is 512 cubic inches, its edge length is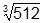 or 8 inches. Its radius is 4 and its volume is
4 thirds pi left paren 4 cubed right paren
The smallest sphere that can be circumscribed about the cube passes through the
vertices of the cube, so its diameter is the length of a diagonal of the cube. Since
the cube’s edge length is 8, its diagonal length is
square root of 8 square plus 8 squared plus 8 squared equals 8 times square root of 3,
the radius of the circumscribed sphere is
4 times square root of 3.
and the volume of the sphere is
4 thirds pi left paren 4 cubed right paren left paren square root of three right paren cubed.
The ratio of the volumes reduces to
1 over square root of 3 cubed equals 1 over 3 times square root of 3.
or 8 inches. Its radius is 4 and its volume is
4 thirds pi left paren 4 cubed right paren
The smallest sphere that can be circumscribed about the cube passes through the
vertices of the cube, so its diameter is the length of a diagonal of the cube. Since
the cube’s edge length is 8, its diagonal length is
square root of 8 square plus 8 squared plus 8 squared equals 8 times square root of 3,
the radius of the circumscribed sphere is
4 times square root of 3.
and the volume of the sphere is
4 thirds pi left paren 4 cubed right paren left paren square root of three right paren cubed.
The ratio of the volumes reduces to
1 over square root of 3 cubed equals 1 over 3 times square root of 3.
Objective 0015
Understand Euclidean geometry.
17. A teacher displays a large sheet of paper in the shape of a sector of a circle and then joins the straight edges with tape. This demonstration would be most appropriate for which of the following purposes?
- introducing a unit on platonic solids
- illustrating the lateral surface area of a cone
- showing that oblique and right solids have the same volume
- indicating the vertices and edges of polyhedra
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
A sector of a circle is formed by a central angle and its subtended arc. When the sector is cut out of the circle and the straight edges are joined, the result is a cone. The area of the sector of the circle is the lateral area of the cone.
Objective 0016
Understand coordinate and transformational geometry.
18. Use the diagram below to answer the question that follows.
the diagram shows triangle a b c and triangle a prime b prime c prime plotted on an x, y graph. in triangle a b c, the coordinates of point a are 2, 4. in triangle a prime b prime c prime, the coordinates of point a prime are 6, 12. both points lie on the line y equals 2 x. points b, c, b prime, and c prime all lie on the line y equals x over 2.
triangle a b c is enlarged to triangle a' b' c' by a point projection from the origin of the coordinate plane as shown in the diagram. What is the ratio of the area of triangle a b c to the area of triangle a' b' c'
- 1 to 4 ratio
- 1 to 9 ratio
- 2 to 3 ratio
- 4 to 9 ratio
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: B.
A point projection, also called a dilation, increases or decreases measurements proportionally. Since each coordinate in left paren 2 comma 4 right paren is multiplied by 3 to get left paren 6 comma 12 right paren the ratio of linear measurements in the two triangles is 1 to 3 ratio The ratio of the areas is the square of the ratio of the linear measures, or 1 to 9 ratio
Objective 0017
Understand the process of collecting, organizing, and representing data.
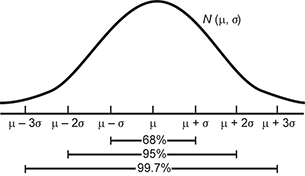
19. Use the normal model below to answer the question that follows.
The model is a normal distribution graph of N mu sigma from mu minus 3 sigma to mu plus 3 sigma. From mu minus sigma to mu plus sigma is dimensioned as 68 percent. From mu minus 2 sigma to mu plus 2 sigma is dimensioned as 95 percent. From mu minus 3 sigma to mu plus 3 sigma is dimensioned as 99.7 percent.
A certain type of dry cat food is packaged by weight in 3-pound (48-ounce) bags. The machine used to fill the bags is set so that, on average, a bag contains 48.5 ounces. The company has determined that the weights of all bags are normally distributed with a standard deviation of 0.5 ounce. If the company ships 200 randomly selected bags to a pet store, about how many bags can be expected to contain less than 3 pounds of cat food?
- 16
- 27
- 32
- 45
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
weights are normally distributed with a mean of 48.5 and standard deviation 0.5, so 50 percent of all weights fall below 48.5 and 34 percent of the weights fall within one standard deviation below the mean, which is between 48 and 48.5. this leaves 16 percent of weights below 48. of 200 randomly selected bags, about 16 percent of them or 0.16 left paren 200 right paren equals 32 can be expected to weigh less than 48 ounces.
Objective 0018
Understand probability and discrete mathematics.
20. If two numbers are selected at random and without replacement from the set left curly bracket 3 comma 5 comma 7 comma 11 comma 13 right curly bracket what is the probability that their product is divisible by 7?
- 1 tenth
- 1 fifth
- 2 fifths
- 1 half
- Answer and Rationale. Enter to expand or collapse. Answer expanded
-
Correct Response: C.
If two numbers are selected without replacement, then there are 5 choices for the first number and 4 choices for the second number, which makes 20 pairs; however, each pair of numbers is counted twice, since choosing 5 first and 11 second, for example, is the same as choosing 11 first and 5 second. Thus, there are really 10 pairs to consider. Since 3, 5, 11, and 13 are not divisible by 7, the only products divisible by 7 are those which have 7 as a factor. There are 4 of these: 3 times 7, 5 times 7 11 times 7, and 13 times 7 Thus, the probability that the product is divisible by 7 is 4 tenths equals 2 fifths.

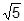 ,
,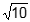 ,
,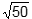 ;
;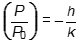 for
P.
Apply the exponential function to both sides of the equation:
for
P.
Apply the exponential function to both sides of the equation:
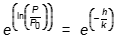 ,
so
,
so
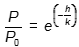 .
Multiply both sides of the equation by P0 to obtain
.
Multiply both sides of the equation by P0 to obtain
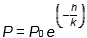 .
.
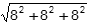 =
= 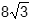 ,
,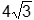 ,
,